为了鼓励市民节约用水，某市自来水公司对每户用水量进行了分段计费，每户每月用水量在规定吨数以下的收费标准相同，规定吨数以上的超过部分收费相同．如表是小明家1﹣4月用水量和交费情况：
月份 1 2 3 4
用水量（吨） 6 8 12 15
费用（元） 12 16 28 37
（1）自来水公司规定用水量为 吨，规定用量的收费标准是 元/吨，超过部分收费 元/吨．
（2）若小明家5月份用水25吨，则应缴多少元水费？
（3）若小明6月份缴水费43元，则6月份他们家用水多少吨？
如图，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B，最低点为M，且S△AMB＝
.
（1）求此抛物线的解析式，并说明这条抛物线是由抛物线y=ax2怎样平移得到的；
（2）如果点P由点A开始沿着射线AB以2cm/s的速度移动，同时点Q由点B开始沿BC边以1cm/s的速度向点C移动，当其中一点到达终点时运动结束；
①在运动过程中，P、Q两点间的距离是否存在最小值，如果存在，请求出它的最小值；
②当PQ取得最小值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是梯形? 如果存在，求出R点的坐标，如果不存在，请说明理由.
李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
（1）如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；
（2）如图2，圆锥的母线长为4cm，底面半径r=
cm，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A；
（3）如图3，是一个没有上盖的圆柱形食品盒，一只蚂蚁在盒外表面的A处，它想吃到盒内表面对侧中点B处的食物，已知盒高10cm，底面圆周长为32cm，A距下底面3cm..
近日某小区计划在中央花园内建造一个圆形的喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰好在水面中心，OA为1.25m，安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA的任一平面上抛物线路径如图所示．为使水流形状较为漂亮，设计成水流在到OA距离lm处达到距水面最大高度2.25m.
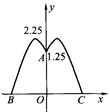
（1）请求出其中一条抛物线的解析式；
（2）如果不计其他因素，那么水池的半径至少要为多少m 才能使喷出水流不致落到池上？
如图，P是⊙O的直径AB延长线上的一点， PC切⊙O于点C，弦CD⊥AB，垂足为点E，若
，
．
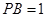求：（1）⊙O的半径；
（2）CD的长；
（3）图中阴影部分的面积．
已知：抛物线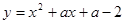
.
（1）求证：不论a取何值时，抛物线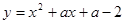与x轴都有两个不同的交点.
（2）设这个二次函数的图象与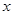
轴相交于A（
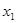，0），B(
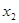，0)，且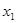、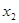的平方和为3，求a的值.