如图所示,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=acm,其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣CB=bcm,M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.
已知 ,求
,求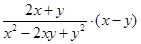 的值.
的值.
解不等式组: ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
如图,平面直角坐标系中O为坐标原点,直线y=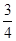 x+6与x轴、y轴分别交于A、B两点,C为OA中点;
x+6与x轴、y轴分别交于A、B两点,C为OA中点;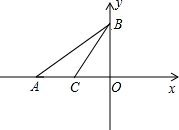
(1)求直线BC解析式;
(2)动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动,同时动点Q从C出发沿线段CB以每秒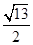 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t(s),求y于t的函数关系式;
(3)在(2)的条件下,以PC为直径作⊙N,求t为何值时直线QM与⊙N相切.
有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC分别表示单独打开一个进水管和单独打开一个出水管时,容器内的水量Q(升)随时间t变化的函数关系.根据图象进行以下探究: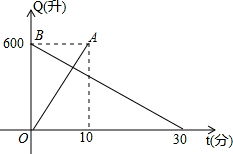
(1)求进水管的进水速度和出水管的出水速度;
(2)求线段BC所表示的Q与t之间的函数关系式,并写出自变量t的取值范围;
(3)现已知水池内有水200升,先打开两个进水管和一个出水管2分钟,再关上一个进水管,直至把容器放满,关上所有水管;3分钟后,同时打开三个出水管,直至把容器中的水放完,画出这一过程的函数图象;并求出在这个过程中容器内的水量Q与t的函数关系式,并写出自变量t的取值范围.