回答下列问题：
（1）如图所示的甲、乙两个平面图形能折什么几何体？
（2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为f，顶点个数为v，棱数为e，分别计算第（1）题中两个多面体的f+v﹣e的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．
如图，已知：AD为△ABC中BC边的中线，CE∥AB交AD的延长线与点E，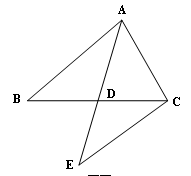
（1）求证：AB=CE；
（2）试判断2AD与(AB+AC) 的大小关系，即2AD
(AB+AC)．（只填“=”、“>”或“<”）
如图，在△ABC中，D是BC边的中点，且AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别是E，F，求证：△ABC是等腰三角形 ．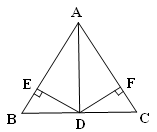
尺规作图：如图，已知点A、点B以及直线l，在直线l上求做一点P，使PA=PB（不写作法，要保留作图痕迹）
如图，在△ABC中，AB="AC," ∠BAD＝30°，AD="AE," 求∠EDC的度数．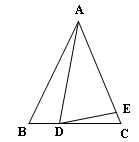
如图，在△ABC中，∠C＝90°，∠A＝36°，DE是线段AB的垂直平分线，交AB于点D，交AC于点E，求∠EBC
的度数 ．