在△ABC中,角A、B、C的对边分别为a,b,c,且满足 ,2bsinA=a,BC边上中线AM的长为
,2bsinA=a,BC边上中线AM的长为 .
.
(Ⅰ)求角A和角B的大小;
(Ⅱ)求△ABC的面积.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如右图所示.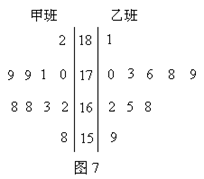
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
(本小题12分)
现向图中所示正方形随机地投掷飞镖,求飞镖落在阴影部分的概率.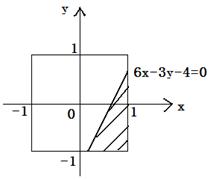
(本小题12分)
为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为 ,第二小组频数为12.
,第二小组频数为12.
(1)第二小组的频率是多少?
(2)样本容量是多少?
(3)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(本小题12分)
从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
| 甲 |
7 |
8 |
6 |
8 |
6 |
5 |
9 |
10 |
7 |
4 |
| 乙 |
9 |
5 |
7 |
8 |
7 |
6 |
8 |
6 |
7 |
7 |
(1)计算甲乙两人射击命中环数的平均数和方差;
(2)比较两人的成绩,然后决定选择哪一人参赛.
(本小题12分)
某企业组织职工观看了文艺晚会.企业中共有3200名职工,其中中、青、老年职工的人数比例为5: 3:2,为了解这次晚会在职工中的影响,现从职工中抽取一个容量为400的样本,应该采用哪种抽样方法更合理?中、青、老年职工应分别抽取多少人?