某工厂因排污比较严重，决定着手整治，一个月时污染度为60，整治后前四个月的污染度如表：
| 月数 |
1 |
2 |
3 |
4 |
… |
| 污染度 |
60 |
31 |
13 |
0 |
… |
污染度为0后，该工厂即停止整治，污染度又开始上升，现用下列三个函数模拟从整治后第一个月开始工厂的污染模式：f（x）=20|x﹣4|（x≥1），
，
，其中x表示月数，f（x）、g（x）、h（x）分别表示污染度．
（1）问选用哪个函数模拟比较合理？并说明理由；
（2）若以比较合理的模拟函数预测，整治后有多少个月的污染度不超过60？
已知函数
，当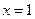
时，有极大值
；
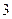（1）求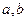
的值；（2）求函数
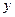的极小值。
求函数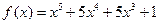
在区间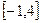
上的最大值与最小值。
求函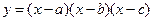数
的导数。
对某校小学生进行心理障碍测试得如下列联表：（其中焦虑、说谎、懒惰都是心理障碍）
| 焦虑 |
说谎 |
懒惰 |
总计 |
|
| 女生 |
5 |
10 |
15 |
30 |
| 男生 |
20 |
10 |
50 |
80 |
| 总计 |
25 |
20 |
65 |
110 |
试说明在这三种心理障碍中哪一种与性别关系最大？
一机器可以按各种不同的速度运转，其生产物件有一些会有缺点，每小时生产有缺点物件的多少随机器运转速度而变化，用x表示转速（单位：转/秒），用y表示每小时生产的有缺点物件个数，现观测得到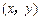
的4组观测值为（8，5），（12，8），（14，9），（16，11）．
（1）假定y与x之间有线性相关关系，求y对x的回归直线方程；
（2）若实际生产中所容许的每小时最大有缺点物件数为10，则机器的速度不得超过多少转/秒．（精确到1转/秒）