为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下面表中所示:
| 是否需要帮助 性别 |
男 |
女 |
合计 |
| 需要 |
50 |
25 |
75 |
| 不需要 |
200 |
225 |
425 |
| 合计 |
250 |
250 |
500 |
(1)请根据上表的数据,估计该地区老年人中,需要志愿者提供帮助的老年人的比例;]
(2)能否在出错的概率不超过1%的前提下,认为该地老年人是否需要帮助与性别有关?并说明理由;
(3)根据(2)的结论,你能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?并说明理由.
附:独立性检验卡方统计量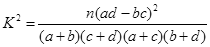 ,其中
,其中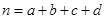 为样本容量,独立性检验临界值表为:
为样本容量,独立性检验临界值表为:
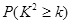 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
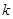 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)已知数列 满足
满足 ,等比数列
,等比数列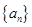 为递增数列,且
为递增数列,且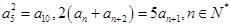 .
.
(1)求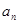 ;
;
(2)令 ,不等式
,不等式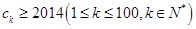 的解集为M,求所有
的解集为M,求所有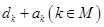 的和.
的和.
(本小题满分12分)如图,在等腰梯形ABCD中,AB//CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面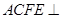 平面ABCD,CF=1.
平面ABCD,CF=1.
(1)求证: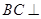 平面ACFE;
平面ACFE;
(2)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为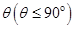 ,试求
,试求 的取值范围.
的取值范围.
(本小题满分12分)已知函数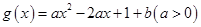 在区间
在区间 上有最小值1和最大值4,设
上有最小值1和最大值4,设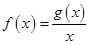 .
.
(1)求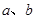 的值;
的值;
(2)若不等式 在区间
在区间 上有解,求实数k的取值范围.
上有解,求实数k的取值范围.
(本小题满分12分)已知函数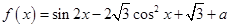 .
.
(1)求函数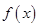 的单调递减区间;
的单调递减区间;
(2)设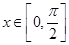 时,函数
时,函数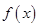 的最小值是
的最小值是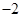 ,求
,求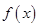 的最大值.
的最大值.
已知f(x)=|x+1|+|x-1|,不等式f(x)<4的解集为M.
(1)求M.
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.