已知对任意平面向量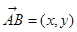 ,把
,把 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转 角得到向量
角得到向量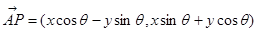 ,叫做把点
,叫做把点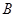 绕点
绕点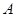 逆时针方向旋转角得到点
逆时针方向旋转角得到点 。
。
(1)已知平面内点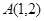 ,点
,点 。把点
。把点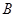 绕点
绕点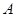 沿逆时针旋转
沿逆时针旋转 后得到点
后得到点 ,求点
,求点 的坐标;
的坐标;
(2)设平面内直线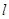 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转 后得到的点组成的直线方程是
后得到的点组成的直线方程是 ,求原来的直线
,求原来的直线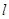 方程。
方程。
已知函数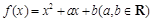 ,
,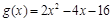 ,且
,且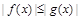 对
对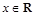 恒成立.
恒成立.
(1)求a、b的值;
(2)若对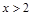 ,不等式
,不等式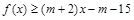 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)记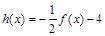 ,那么当
,那么当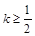 时,是否存在区间
时,是否存在区间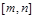 (
(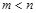 ),使得函数
),使得函数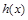 在区间
在区间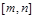 上的值域恰好为
上的值域恰好为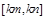 ?若存在,请求出区间
?若存在,请求出区间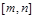 ;若不存在,请说明理由.
;若不存在,请说明理由.
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
设函数
(1)求函数 的最小正周期;
的最小正周期;
(2)设函数 对任意
对任意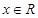 ,有
,有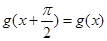 ,且当
,且当 时,
时,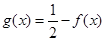 ;求函数
;求函数 在
在 上的解析式。
上的解析式。
已知 其中
其中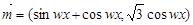 ,
,
 ,若
,若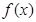 图象中相邻的两条对称轴间的距离不小于
图象中相邻的两条对称轴间的距离不小于 。
。
(1)求 的取值范围
的取值范围
(2)在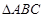 中,a,b,c分别为角A,B,C的对边,
中,a,b,c分别为角A,B,C的对边,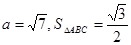 。当
。当 取最大值时,f(A)=1,求b,c的值。
取最大值时,f(A)=1,求b,c的值。
(1)已知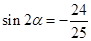 ,
,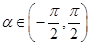 ,求
,求 的值;
的值;
(2)已知 .
.
求 的值.
的值.