如图,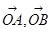 为平面的一组基向量,
为平面的一组基向量,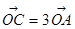 ,
,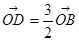 ,
, 与
与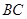 交与点
交与点

(1)求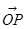 关于
关于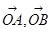 的分解式;(2)设
的分解式;(2)设 ,
, ,求
,求 ;
;
(3)过 任作直线
任作直线 交直线
交直线 于
于 两点,设
两点,设
 ,
,
( )求
)求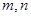 的关系式。
的关系式。
某工厂统计资料显示,产品次品率p与日产量x(单位:件,x∈N*,1≤x≤96)的关系如下:
又知每生产一件正品盈利a(a为正常数)元,每生产一件次品就损失 元.
元.
(注:次品率p= ×100%,正品率=1-p)
×100%,正品率=1-p)
(1)将该厂日盈利额T(元)表示为日产量x的函数;
(2)为了获得最大盈利,该厂的日产量应定为多少件?
设a>0,b>0,a+b=1.
(1)证明:ab+ ≥4
≥4 ;
;
(2)探索猜想,并将结果填在以下括号内:
a2b2+ ≥();a3b3+
≥();a3b3+ ≥();
≥();
(3)由(1)(2)归纳出更一般的结论,并加以证明.
已知a、b∈(0,+∞),且a+b=1,求证:
(1)a2+b2≥ ;
;
(2) +
+ ≥8;
≥8;
(3) +
+  ≥
≥ ;
;
(4) 
 ≥
≥ .
.
(1)已知0<x< ,求x(4-3x)的最大值;
,求x(4-3x)的最大值;
(2)点(x,y)在直线x+2y=3上移动,求2x+4y的最小值.
若-4<x<1,求 的最大值.
的最大值.