已知椭圆 的焦点分别为F1(
的焦点分别为F1( ,0)、F2(
,0)、F2( ,0),长轴长为6,设直线
,0),长轴长为6,设直线 交椭圆
交椭圆 于A、B两点.
于A、B两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)求 的面积.
的面积.
甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为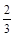 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为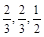 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响.
(1)若用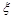 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量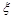 分布列和数学期望;
分布列和数学期望;
(2)用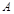 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为 ”,用
”,用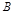 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求 .
.
在城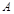 的西南方向上有一个观测站
的西南方向上有一个观测站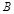 ,在城
,在城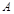 的南偏东
的南偏东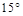 的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城
的方向上有一条笔直的公路,一辆汽车正沿着该公路上向城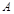 驶来.某一刻,在观测站
驶来.某一刻,在观测站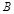 处观测到汽车与
处观测到汽车与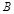 处相距
处相距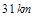 ,在
,在 分钟后观测到汽车与
分钟后观测到汽车与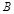 处相距
处相距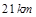 .若汽车速度为
.若汽车速度为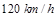 ,求该汽车还需多长时间才能到达城
,求该汽车还需多长时间才能到达城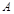 ?
?
如图,已知四棱锥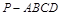 的底面
的底面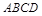 是正方形,侧棱
是正方形,侧棱 底面
底面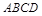 ,
,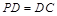 ,
,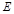 是
是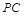 的中点.
的中点.
(1)证明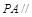 平面
平面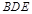 ;
;
(2)求二面角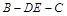 的余弦值.
的余弦值.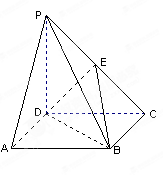
在数列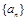 中,
中,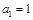 ,且对任意的
,且对任意的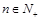 ,都有
,都有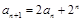 .
.
(1)求证:数列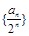 是等差数列;
是等差数列;
(2)设数列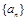 的前
的前 项和为
项和为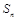 ,求证:对任意的
,求证:对任意的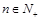 ,
,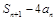 都为定值.
都为定值.
已知函数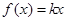 ,
,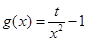 ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.