某百货大搂服装柜在销售中发现:“七彩”牌童装平均每天可售出20件,每件盈利40元.为了迎接“元旦”,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.
(1)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
(2)用配方法说明:要想盈利最多,每件童装应降价多少元?
如图,∠α与∠β有公共顶点,且∠α两边与∠β的两边互相垂直,∠α= ∠β.试求∠α,∠β的度数.
∠β.试求∠α,∠β的度数.
在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的。如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角. 从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D 的飞行方向角为145°,试求AB与AC之间夹角为多少度?AD与AC之间夹角为多少度?并画出从A飞出且方向角为105°的飞行线.
小华从A点出发向北偏东50°方向走了80米到达B地,从B 地他又向西走了100米到达C地.
(1)用1:2000的比例尺(即图上1cm等于实际距离20米)画出示意图;
(2)用刻度尺和量角器量出AC的距离,以及C点的方向角;
(3)回答C点距A点的实际距离是多少(精确到1米),C点的方向角为多少.(精确到1°).
如图所示,A、B两条海上巡逻艇同时发现海面上有一不明物体,A艇发现该不明物体在它的东北方向,B艇发现该不明物体在它的南偏东60°的方向上, 请你试着在图中确定这个不明物体的位置.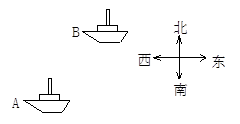
直线AB、CD相交于O,∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线. 画出图形并求出∠BOD和∠DOF的度数.