一名足球守门员连续往返跑，从守门的位置出发，向前记为正，返回记为负，他记录如下(单位：m): +5，-3，+10，-6，-4，+8，-10.
(1)守门员最后的位置在哪里？
(2)守门员一共跑了多少米？
(3)守门员离开守门的位置最远是多少米？他是在跑完第几次后到了最远的位置？
如图，二次函数
的图象与x轴交于点A（﹣1，0），B（2，0），与y轴相交于点C．
（1）求二次函数的解析式；
（2）若点E是第一象限的抛物线上的一个动点，当四边形ABEC的面积最大时，求点E的坐标，并求出四边形ABEC的最大面积；
（3）若点M在抛物线上，且在y轴的右侧．⊙ M与y轴相切，切点为D．以C，D，M为顶点的三角形与△AOC相似，求点M的坐标．
如图，已知△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC，AD=AE．连接BD交AE于M，连接CE交AB于N，BD与CE交点为F，连接AF．
（1）如图1，求证：BD⊥CE；
（2）如图1，求证：FA是∠CFD的平分线；
（3）如图2，当AC=2，∠BCE=15°时，求CF的长．
已知：如图，一次函数
的图象与反比例函数
的图象交于A、B两点，且点A的坐标为（1，m）．
（1）求反比例函数的表达式；
（2）点C（n，1）在反比例函数的图象上，求△AOC的面积；
（3）在x轴上找出点P，使△ABP是以AB为斜边的直角三角形，请直接写出所有符合条件的点P的坐标．
已知，正方形ABCD的边长为6，点E为BC的中点，点F在AB边上，且∠EDF＝45°．
（1）利用画图工具，在右图中画出满足条件的图形；
（2）猜想tan∠ADF的值，并写出求解过程．
已知：如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，经过B、D两点的⊙O交AB 于点E，交BC于点F， EB为⊙O的直径．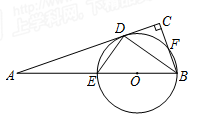
（1）求证：AC是⊙O的切线；
（2）当BC=2，cos∠ABC=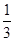
时，求⊙O的半径．