已知正方形ABCD中，AB＝BC＝CD＝AD=10cm，动点P，Q分别从点B，C同时出发沿正
方形的四周运动．设点P的运动速度为2cm/s，点Q的运动速度为3cm/s，设点P，Q运动的时间为t（s）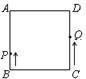
（1）若点P，Q作相向运动，且它们第一次相遇在AD边上，求t的值．
（2）在（1）中点P，Q第一次相遇后继续运动，到第2次相遇，第3次相遇，…，求第100次相遇时，
相遇地点在正方形ABCD哪条边上，请写出计算过程．
（3）若点P，Q作同向运动，求它们相遇时t的值．
如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在点E处，连接DE．若DE：AC=3：5，则
的值为 ．
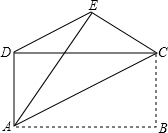
用适当的方法解下列方程：
（1）
（2）
计算
（1）（
－
）0－
＋
（2）
如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．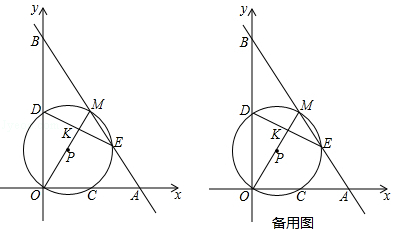
（1）若点M的坐标为（3，4），
①求A，B两点的坐标；
②求ME的长．
（2）若
，求∠OBA的度数．
（3）设tan∠OBA=x（0＜x＜1），
，直接写出y关于x的函数解析式．
请同学们认真阅读下面的一段文字材料，然后解答题目中提出的有关问题．
为解方程
，我们可以将
视为一个整体，然后设
，则原方程可化为
①
解得
，
，当y=1时，
，∴
，
；
当y=4时，
，∴
，
，∴原方程的解为
=
，
=－，
=
，
=－．
解答问题：
（1）填空：在由原方程得到方程①的过程中，利用_________法达到了降次的目的，体现了_________的数学思想．
（2）解方程
．