某商场将每件进价为160元的某种商品原来按每件200元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降低2元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利润y元.
①若商场经营该商品一天要获利润4320元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,当x取何值时,商场获利润最大?并求最大利润值.
(本题8分)某服装店老板到厂家选购A、B两种型号的服装,它们的进价及获利如右表所示.
(1)根据市场需求,服装店老板决定,购进B型服装的数量要比购进A型服装数量的2倍少3件,且A型服装最多可购进28件,这样服装全部售出后,可使总的获利不少于1534元.问有几种进货方案?请求出所有的进货方案.
(2)采用哪种方案时,可获得最大利润,最大利润为多少?
| 型号 |
A |
B |
| 进价(元/件) |
90 |
120 |
| 获利(元/件) |
20 |
22 |
(本题6分)小青同学想利用影长测量学校旗杆AB的高度.某一时刻他测得长1米的标杆的影长为1.4米,与此同时他发现旗杆AB的一部分影子BD落在地面上,另一部分影子CD落在楼房的墙壁上,分别测得其长度为11.2米和2米,如图所示.请你帮他求出旗杆AB的高度.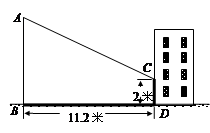
(本题6分)如图,直线AG交□ABCD的对角线BD于点E,交BC于点F,交DC的延长线于G.(1)请找出一个与△ADG相似的三角形,并说明理由;(2)若点F恰为BC的中点,且△BEF的面积为6,求△ADE的面积.
(本题6分)已知格点△ABC.
(1)画出与△ABC相似的格点△A1B1C1,使△A1B1C1与△ABC的相似比为2;
(2)画出与△ABC相似的格点△A2B2C2,使△A2B2C2与△ABC的相似比为 ;
;
(3)格点△A1B1C1和格点△A2B2C2的相似比为.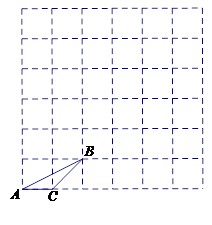
计算(每小题4分,共16分)
(1)求不等式组  的整数解;
的整数解;
(2)解方程: =
= ;
;
(3) =
= +2;
+2;
(4)先化简 ÷
÷ ,再从2,1,-1中选一个你认为合适的数作为x的值代入求值.
,再从2,1,-1中选一个你认为合适的数作为x的值代入求值.