(本题6分)小青同学想利用影长测量学校旗杆AB的高度.某一时刻他测得长1米的标杆的影长为1.4米,与此同时他发现旗杆AB的一部分影子BD落在地面上,另一部分影子CD落在楼房的墙壁上,分别测得其长度为11.2米和2米,如图所示.请你帮他求出旗杆AB的高度.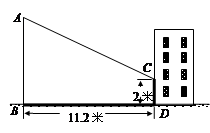
陈老师为学校购买运动会的奖品后,回学校向后勤 处王老师交帐说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定搞错了.”
处王老师交帐说:“我买了两种书,共105本,单价分别为8元和12元,买书前我领了1500元,现在还余418元.”王老师算了一下,说:“你肯定搞错了.”
(1)王老师为什么说他搞错了?试用方程的知识给予解释.
(2)陈老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本。但笔记本的单价已模糊不清,只能辩认出应为小于8元的整数,笔记本的单价可能为多少元?
铜仁市某中学在一次健康知识测试中,抽取部分学生成绩(分数为整数,满分100分)为样本,绘制成绩统计图,如图所示,请结合统计图回答下列问题: 
(1)本次测试中抽样的学生有多少人?
(2)分数在90.5~100.5这一组的人数是多少?
(3)估计这次考试出现次数最多的那个分数落在哪一组内?
李斌和张强在周末骑自行车从长炼出发去临湘玩,出发前他俩一起算了一下:如果每小时骑10km,上午10时才能到达;如果每小时骑15km,则上午9时40分就能到达。求长炼到临湘的路程。
解不等式:
解方程: