佳佳果品店在批发市场购买某种水果销售，第一次用1200元购进若干千克，并以每千克8元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了10%，用1452元所购买的数量比第一次多20千克，以每千克9元售出100千克后，因出现高温天气，水果不易保鲜，为减少损失，便降价50%售完剩余的水果．
（1）求第一次水果的进价是每千克多少元？
（2）该果品店在这两次销售中，总体上是盈利还是亏损？盈利或亏损了多少元？
如图，△ABC的边AB为⊙O的直径，BC与圆交于点D，D为BC的中点，过D作DE⊥AC于E．
（1）求证：AB=AC；
（2）求证：DE为⊙O的切线；
（3）若AB=13，sinB=
，求CE的长．
如图：已知A（-4，n）、B（2，-4）是一次函数y1=kx+b的图象与反比例函数y2=
的图象
的两个交点．
（1）求反比例函数和一次函数的解折式．
（2）求直线AB与x轴的交点C的坐标及△AOB的面积．
（3）求不等式y1<y2
的解集（请直接写出答案）．
如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．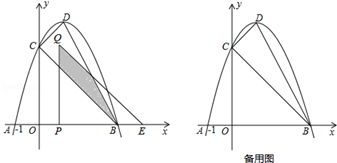
（1）求点B，C的坐标；
（2）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．
某商店欲购进甲、乙两种商品，已知甲的进价是乙的进价的一半，进3件甲商品和1件乙商品恰好用200元．甲、乙两种商品的售价每件分别为80元、130元，该商店决定用不少于6710元且不超过6810元购进这两种商品共100件．
（1）求这两种商品的进价．
（2）该商店有几种进货方案？哪种进货方案可获得最大利润，最大利润是多少？
如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．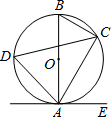
（1）求证：AE是⊙O的切线
（2）当BC=4时，求劣弧AC的长