在斜三角形ABC中,角A,B,C的对边分别为a,b,c.
(Ⅰ)若2sin Acos C=sin B,求 的值;
的值;
(Ⅱ)若sin(2A+B)=3sin B,求 的值.
的值.
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2); (Ⅱ)求随机变量ξ的分布列和它的数学期望.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求

 +2的概率.
+2的概率.
已知a=2( ,
, ),b=(
),b=( ,
, )(其中0<
)(其中0< <1),函数
<1),函数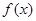 =a·b,若直线
=a·b,若直线 =
= 是函数
是函数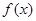 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)试求 的值;
的值;
(Ⅱ)若函数y= 的图象是由y=
的图象是由y=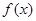 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移 个单位长度得到,求y=
个单位长度得到,求y= 的单调递增区间.
的单调递增区间.
已知函数
(1)当 时,如果函数
时,如果函数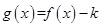 仅有一个零点,求实数
仅有一个零点,求实数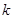 的取值范围.
的取值范围.
(2)当 时,比较
时,比较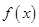 与1的大小.
与1的大小.
(3)求证: