如图,在△ABC中,A(-2,3)、B(-3,1)、C(-1,2).
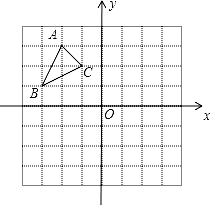
(1)将△ABC向右平移4个单位长度,画出平移后的△A1B1C1.
(2)画出△ABC关于x轴对称的△A2B2C2.
(3)将△ABC绕着原点O旋转180°,画出旋转后的△A3B3C3.
(4)△A1B1C1与△A3B3C3关于点 成 对称(填“轴对称”或“中心对称”).
已知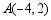 、
、 两点是一次函数
两点是一次函数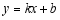 和反比例函数
和反比例函数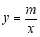 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求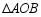 的面积;
的面积;
(3)观察图象,直接写出不等式 的解集.
的解集.
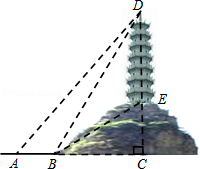
如图,某人为了测量小山顶上的塔 的高,他在山下的点
的高,他在山下的点 处测得塔尖点
处测得塔尖点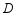 的仰角为
的仰角为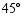 ,再沿
,再沿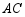 方向前进
方向前进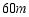 到达山脚点
到达山脚点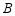 ,测得塔尖点
,测得塔尖点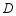 的仰角为
的仰角为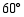 ,塔底点
,塔底点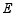 的仰角为
的仰角为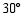 ,求塔
,求塔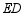 的高度.(结果保留根号)
的高度.(结果保留根号)
小明随机调查了若干市民租用共享单车的骑车时间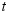 (单位:分),将获得的数据分成四组,绘制了如下统计图
(单位:分),将获得的数据分成四组,绘制了如下统计图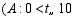 ,
,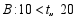 ,
,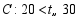 ,
,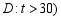 ,根据图中信息,解答下列问题:
,根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示 组的扇形统计图的圆心角的度数,补全条形统计图;
组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从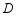 组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
如图, 平分
平分 ,
, ,垂足为点
,垂足为点 ,
, .
.
求证: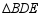 是等腰三角形.
是等腰三角形.

如图1,已知二次函数 、 、 为常数, 的图象过点 和点 ,函数图象最低点 的纵坐标为 ,直线 的解析式为 .
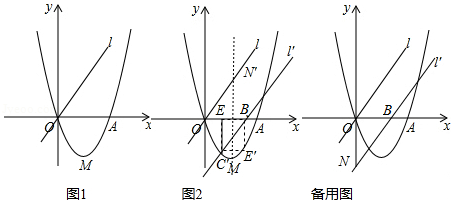
(1)求二次函数的解析式;
(2)直线 沿 轴向右平移,得直线 , 与线段 相交于点 ,与 轴下方的抛物线相交于点 ,过点 作 轴于点 ,把 沿直线 折叠,当点 恰好落在抛物线上点 时(图 ,求直线 的解析式;
(3)在(2)的条件下, 与 轴交于点 ,把 绕点 逆时针旋转 得到△ , 为 上的动点,当△ 为等腰三角形时,求符合条件的点 的坐标.