如图,四面体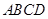 中,
中,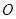 是
是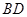 的中点,
的中点,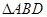 和
和 均为等边三角形,
均为等边三角形,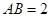 ,
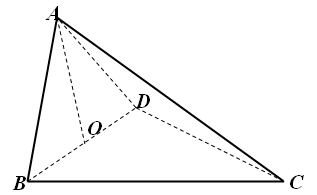
,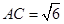 .
.
(Ⅰ)求证: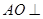 平面
平面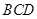 ;
;
(Ⅱ)求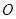 点到平面
点到平面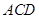 的距离.
的距离.
某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数 ,并将完成生产任务所需时间超过 和不超过 的工人数填入下面的列联表:
|
超过 |
不超过 |
|
|
第一种生产方式 |
||
|
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附: ,
|
|
|
|
|
|
|
|
|
|
等比数列 中, .
(1)求 的通项公式;
(2)记 为 的前 项和.若 ,求 .
已知函数 .
(Ⅰ)若f(x)在x=x 1,x 2(x 1≠x 2)处导数相等,证明:f(x 1)+f(x 2)>8−8ln2;
(Ⅱ)若a≤3−4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.
如图,已知点P是y轴左侧(不含y轴)一点,抛物线C:y 2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.

(Ⅰ)设AB中点为M,证明:PM垂直于y轴;
(Ⅱ)若P是半椭圆x 2+ =1(x<0)上的动点,求△PAB面积的取值范围.
已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1−bn)an}的前n项和为2n2+n.
(Ⅰ)求q的值;
(Ⅱ)求数列{bn}的通项公式.