在平面直角坐标系 O
O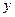 中,直线
中,直线 与抛物线
与抛物线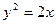 相交于
相交于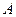 、
、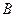 两点。
两点。
(Ⅰ)求证:“如果直线 过点
过点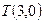 ,那么
,那么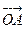
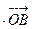 =
=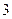 ”是真命题;
”是真命题;
(Ⅱ)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
(文科)已知中心在原点,焦点在x轴上的椭圆的离心率为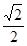 ,
, 为其焦点,一直线过点
为其焦点,一直线过点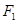 与椭圆相交于
与椭圆相交于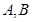 两点,且
两点,且 的最大面积为
的最大面积为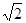 ,求椭圆的方程。
,求椭圆的方程。
(理科)在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO.求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;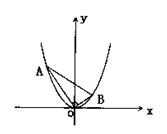
(文科)已知椭圆E: ,点P
,点P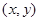 是椭圆上一点。
是椭圆上一点。
(1)求 的最值。
的最值。
(2)若四边形ABCD内接于椭圆E,点A的横坐标为5,点C的纵坐标为4,求四边形面积的最大值。
(理科)如图,已知椭圆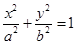 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线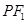 和
和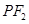 与椭圆的交点分别为
与椭圆的交点分别为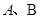 和
和 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线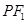 、
、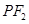 的斜率分别为
的斜率分别为 、
、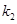 ,证明
,证明 ;
;
(Ⅲ)是否存在常数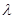 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求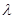 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(文科)如图,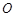 为坐标原点,椭圆
为坐标原点,椭圆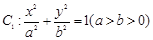 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ;双曲线
;双曲线
 的左、右焦点分别为
的左、右焦点分别为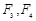 ,离心率为
,离心率为 .已知
.已知 且
且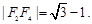

(Ⅰ)求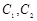 的方程;
的方程;
(Ⅱ)过 作
作 的不垂直于
的不垂直于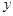 轴的弦
轴的弦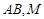 为
为 的中点.当直线
的中点.当直线 与
与 交于
交于 两点时,求四边形
两点时,求四边形 面积的最小值.
面积的最小值.