给出 下面的数表序列:
下面的数表序列:
其中表n(n="1,2,3" 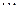 )有n行,第1行的n个数是1,3,5,
)有n行,第1行的n个数是1,3,5,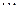 2n-1,从第2行起
2n-1,从第2行起 ,每行中的每个数都等
,每行中的每个数都等 于它肩上的两数之和。
于它肩上的两数之和。
(I)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表n(n≥3)(不要求证明);
(II)每个数列中最后一行都只有一个数,它们构成数列1,4,12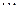
 ,记此数列为
,记此数列为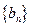 求和:
求和: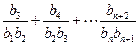
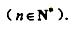
如图所示,在多面体 ,四边形 , 均为正方形, 为 的中点,过 的平面交 于 .

(Ⅰ)证明:
;
(Ⅱ)求二面角
余弦值.
设
,
是曲线
在点
处的切线与
轴交点的横坐标.
(Ⅰ)求数列
的通项公式;
(Ⅱ)记
,证明
.
已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(Ⅰ)求第一次检测出的是次品且第二次检测出的是正品的概率;
(Ⅱ)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求
的分布列和均值(数学期望).
在 中, ,点 在 边上, ,求 的长.
已知函数 .
.
(Ⅰ)若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(Ⅱ)若存在 使关于
使关于 的方程
的方程 有四个不同的实根,求实数
有四个不同的实根,求实数 的取值范围.
的取值范围.