已知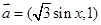 ,
,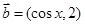 .
.
(1)若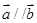 ,求
,求 的值;
的值;
(2)若 ,求
,求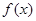 的单调递增区间.
的单调递增区间.
(本小题满分12分)关于x的二次方程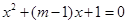 在区间
在区间 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
(本小题满分12分)已知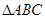 中, 角
中, 角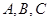 对边分别为
对边分别为 ,已知
,已知 .
.
(1)若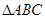 的面积等于
的面积等于 ,求
,求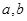
(2)若 ,求
,求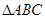 的面积.[来源
的面积.[来源
(本小题满分12分)设函数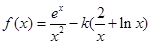 (k为常数,e=2.718 28…是自然对数的底数).
(k为常数,e=2.718 28…是自然对数的底数).
(1)当 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若函数 在(0,2)内存在两个极值点,求k的取值范围.
在(0,2)内存在两个极值点,求k的取值范围.
(本小题满分12分)已知曲线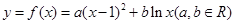 在点
在点 处的切线的斜率为1.
处的切线的斜率为1.
(1)若函数f(x)的图象在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)当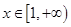 时,不等式
时,不等式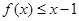 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(本小题满分12分)抛物线 的焦点为F,过点F的直线交抛物线于A,B两点.
的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若 ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.