对于定义域为 的函数
的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间 ,使
,使 在
在 上的值域为
上的值域为 ;那么把
;那么把 (
( )叫闭函数,且条件②中的区间
)叫闭函数,且条件②中的区间 为
为 的一个“好区间”.
的一个“好区间”.
(1)求闭函数 的“好区间”;
的“好区间”;
(2)若 为闭函数
为闭函数 的“好区间”,求
的“好区间”,求 、
、 的值;
的值;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围.
的取值范围.
某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励40慧币;第二种,闯过第一关奖励4慧币,以后每一关比前一关多奖励4慧币;第三种,闯过第一关奖励0.5慧币,以后每一关比前一关奖励翻一番(即增加1倍),游戏规定:闯关者须于闯关前任选一种奖励方案.
(1)设闯过n(n∈N*,且n≤12)关后三种奖励方案获得的慧币依次为An,Bn,Cn,试求出An,Bn,Cn的
表达式;
(2)如果你是一名闯关者,为了得到更多的慧币,你应如何选择奖励方案?
已知数列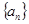 前n项和
前n项和 =
=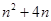 (
( ), 数列
), 数列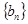 为等比数列,首项
为等比数列,首项 =2,公比为q (q>0) 且满足
=2,公比为q (q>0) 且满足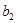 ,
, ,
,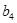 为等差数列。
为等差数列。
(1)求数列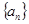 ,
,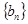 的通项公式;
的通项公式;
(2)设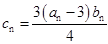 ,记数列
,记数列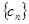 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
在 中,角
中,角 ,
, ,
, 对应的边分别是
对应的边分别是 ,
, ,
, .已知
.已知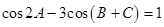 .
.
(1)求角 的大小;
的大小;
(2)若 的面积
的面积 ,
, ,求
,求 的值.
的值.
已知等差数列 的前n项和为
的前n项和为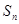 ,
,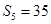 ,
, 和
和 的等差中项为13.
的等差中项为13.
(1)求 及
及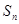 ;
;
(2)令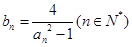 ,求数列
,求数列 的前n项和
的前n项和 。
。
已知函数
(1)求函数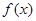 的最小正周期;
的最小正周期;
(2)求函数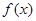 在区间
在区间 上的最大值和最小值,并求此时
上的最大值和最小值,并求此时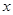 的值.
的值.