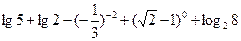已知数列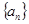 前n项和
前n项和 =
=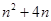 (
( ), 数列
), 数列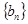 为等比数列,首项
为等比数列,首项 =2,公比为q (q>0) 且满足
=2,公比为q (q>0) 且满足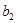 ,
, ,
,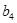 为等差数列。
为等差数列。
(1)求数列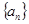 ,
,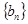 的通项公式;
的通项公式;
(2)设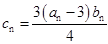 ,记数列
,记数列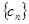 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
(本小题满分13分)
有一批单放机原价为每台80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一台减4元,买两台每台减8元,买三台每台减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一台单放机,问选择哪个商场购买比较划算?
(本小题满分12分)
已知函数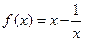
1)讨论并证明函数 )在区间
)在区间 的单调性;
的单调性;
2)若对任意的 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)
已知函数
1)求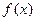 的定义域与值域;
的定义域与值域;
2)判断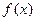 的奇偶性;
的奇偶性;
3)讨论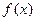 的单调性。
的单调性。
(本小题满分12分)
已知函数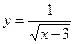 的定义域为集合A,
的定义域为集合A,  的值域为集合B.
的值域为集合B.
(1)若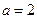 ,求
,求 ;
;
(2) 若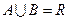 ,求实数
,求实数 的取值范围。
的取值范围。
解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.
16、(本题共两小题,每小题6分,共12分)
(1)求值: