某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,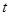 小时内供水总量为
小时内供水总量为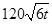 吨(
吨(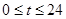 ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(本小题满分14分)
已知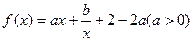 的图像在点
的图像在点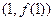 处的切线与直线
处的切线与直线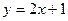 平行.
平行.
(1)求a,b满足的关系式;
(2)若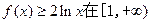 上恒成立,求a的取值范围;
上恒成立,求a的取值范围;
(3)证明: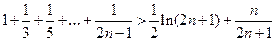 (
(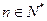 )
)
(本小题满分14分)
已知数列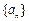 满足:
满足: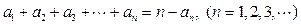
(1)求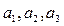 的值;
的值;
(2)求证:数列 是等比数列;
是等比数列;
(3)令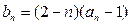 (
(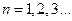 ),如果对任意
),如果对任意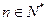 ,都有
,都有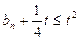 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知x=4是函数f(x)=alnx+x2-12x+11的一个极值点.
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
(本小题满分12分)
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10 km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.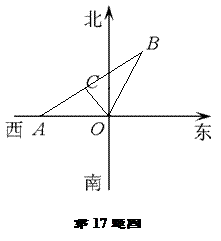
(本小题满分12分)
如图,设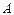 是单位圆和
是单位圆和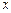 轴正半轴的交点,
轴正半轴的交点,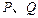 是单位圆上的两点,
是单位圆上的两点, 是
是
坐标原点,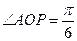 ,
,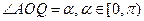 .
.
(1)若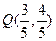 ,求
,求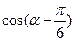 的值;
的值;
(2)设函数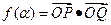 ,求
,求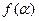 的值域.
的值域.