如图，在三棱柱ABC－A1B1C1中，C1C⊥底面ABC，AC＝BC＝CC1＝2，AC⊥BC，点D是AB的中点．
（1）求证：AC1∥平面CDB1；
（2）求四面体B1C1CD的体积．
【选修4—5：不等式选讲】
已知函数
．
（I）求
的取值范围；
（II）求不等式≥
的解集．
【选修4—4：坐标系与参数方程】
已知圆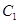
的参数方程为
（
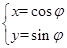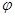为参数），以坐标原点
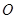为极点，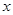
轴的正半轴为极轴建立极坐标系，圆
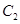的极坐标方程为
.
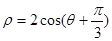（I）将圆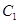的参数方程化为普通方程，将圆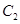的极坐标方程化为直角坐标方程；
（II）圆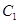、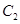是否相交，若相交，请求出公共弦的长；若不相交，请说明理由.
已知函数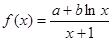
在点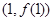
处的切线方程为
．
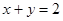（I）求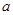
，
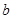的值；
（II）若对函数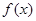
定义域内的任一个实数
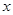，都有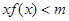
恒成立，求实数
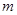的取值范围．
设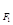
,
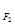分别是椭圆E：
+
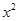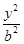=1（0﹤b﹤1）的左、右焦点，过
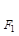的直线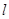
与E相交于A、B两点，且
，
，
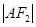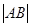成等差数列。
（Ⅰ）求；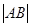
（Ⅱ）若直线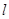的斜率为1，求b的值。
如图，已知四棱锥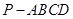
的底面为等腰梯形，
∥
,
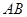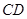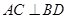,垂足为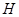
，
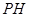是四棱锥的高。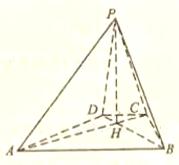
（Ⅰ）证明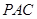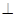：平面
平面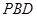
；
（Ⅱ）若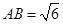
,
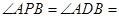60°,求四棱锥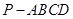的体积。