在 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, 且
且 .
.
(1)求 的面积;
的面积;
(2)若 ,求角
,求角 .
.
(本小题满分14分)
设函数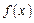 的定义域为R,当x<0时,
的定义域为R,当x<0时,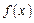 >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有 .
.
(1)求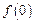 ,判断并证明函数
,判断并证明函数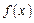 的单调性;
的单调性;
(2)数列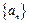 满足
满足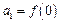 ,且
,且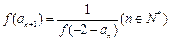 ,
,
①求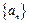 通项公式;
通项公式;
②当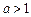 时,不等式
时,不等式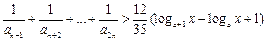 对不小于2的正整数
对不小于2的正整数
恒成立,求x的取值范围.
(本小题满分14分)
已知椭圆 的焦点F与抛物线C:
的焦点F与抛物线C: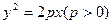 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab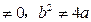 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为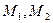 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要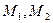 存在
存在
且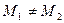 )直线
)直线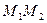 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
(本小题满分14分)
已知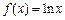 ,
,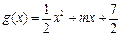 (
(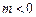 ),直线
),直线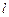 与函数
与函数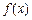 、
、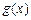 的图像都相切,且与函数
的图像都相切,且与函数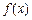 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线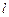 的方程及
的方程及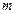 的值;
的值;
(2)若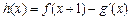 (其中
(其中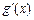 是
是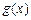 的导函数),求函数
的导函数),求函数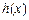 的最大值;
的最大值;
(3)当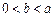 时,比较
时,比较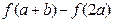 与
与 .
.
(本小题满分14分)
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,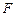 为
为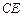 上的点,且BF
上的点,且BF
⊥平面ACE. (1)求证:AE⊥BE;
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试
在线段CE上确定一点N,使得MN∥平面DAE.
(本小题满分12分)
已知集合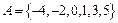 ,在平面直角坐标系中,点
,在平面直角坐标系中,点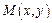 的坐标x∈A,y∈A.计算:
的坐标x∈A,y∈A.计算:
(1)点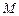 正好在第二象限的概率;
正好在第二象限的概率;
(2)点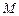 不在x轴上的概率;
不在x轴上的概率;
(3)点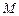 正好落在区域
正好落在区域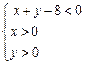 上的概率.
上的概率.