已知以点 为圆心的圆经过点
为圆心的圆经过点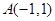 和
和 ,线段
,线段 的垂直平分线交圆于点
的垂直平分线交圆于点 和
和 ,且
,且 .
.
(1)求直线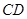 的方程;
的方程;
(2)求圆 的方程.
的方程.
设函数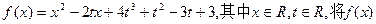 的最小值记为g(t).
的最小值记为g(t).
(1)求g(t)的表达式;
(2)讨论g(t)在区间[-1,1]内的单调性;
(3)当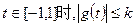 恒成立,其中k为正数,求k的取值范围.
恒成立,其中k为正数,求k的取值范围.
如图,在正三棱柱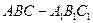 中,
中, 分别是
分别是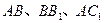 的中点,
的中点,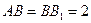 .
.
(Ⅰ)在棱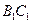 上是否存在点
上是否存在点 使
使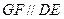 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;
(Ⅱ)求截面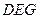 与底面
与底面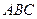 所成锐二面角的正切值.
所成锐二面角的正切值.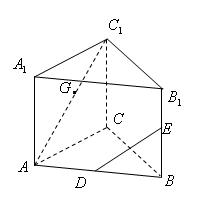
已知向量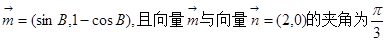 ,其中A、B、C是△ABC的内角.
,其中A、B、C是△ABC的内角.
(1)求角B的大小;
(2)求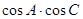 的取值范围.
的取值范围.
某学科的试卷中共有12道单项选择题,(每个选择题有4个选项,其中仅有一个选项是正确的,答对得5分,不答或答错得0分)。某考生每道题都给出了答案,已确定有8道题答案是正确的,而其余的题中,有两道题每题都可判断其两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜。对于这12道选择题,试求:
(1)该考生得分为60分的概率;
(2)该考生所得分数ξ的分布列及数学期望Eξ.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.