设 的内角
的内角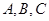 所对边的长分别是
所对边的长分别是 ,且
,且 ,
, 的面积为
的面积为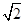 ,求
,求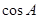 与
与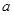 的值.
的值.
已知双曲线 的左、右两个顶点分别为
的左、右两个顶点分别为 .曲线
.曲线 是以
是以 两点为短轴端点,离心率为
两点为短轴端点,离心率为 的椭圆.设点
的椭圆.设点 在第一象限且在曲线
在第一象限且在曲线 上,直线
上,直线 与椭圆
与椭圆 相交于另一点
相交于另一点 .
.
(1)设点 的横坐标分别为
的横坐标分别为 ,证明:
,证明: ;
;
(2)设 与
与 (其中
(其中 为坐标原点)的面积分别为
为坐标原点)的面积分别为 与
与 ,且
,且 ,求
,求 的最大值.
的最大值.
已知函数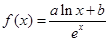 (
( 为常数,无理数
为常数,无理数 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线方程是
处的切线方程是 .
.
(1)求 的值;
的值;
(2)证明不等式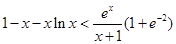 .
.
已知圆 ,经过椭圆
,经过椭圆 的右焦点
的右焦点 及上顶点
及上顶点 ,过圆外一点
,过圆外一点 倾斜角为
倾斜角为 的直线
的直线 交椭圆于
交椭圆于 两点.
两点.
(1)求椭圆的方程;
(2)若右焦点 在以线段CD为直径的圆
在以线段CD为直径的圆 的内部,求
的内部,求 的取值范围.
的取值范围.
已知数列 的前
的前 项和
项和 满足
满足 ,其中
,其中 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知函数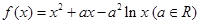 .
.
(1)讨论函数 的单调性;
的单调性;
(2)求函数 在区间
在区间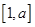 上的最小值.
上的最小值.