选修4-4:坐标系与参数方程
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线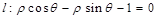 和曲线
和曲线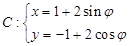 (
(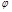 为参数).
为参数).
(1)将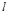 与
与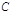 的方程化为普通方程;
的方程化为普通方程;
(2)判定直线l与曲线 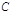 是否相交,若相交求出
是否相交,若相交求出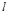 被
被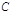 截得的弦长.
截得的弦长.
已知函数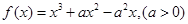
(Ⅰ)若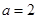 ,求函数
,求函数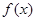 的单调区间与极值;
的单调区间与极值;
(Ⅱ)已知方程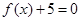 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数 的取值范围
的取值范围
已知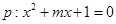 有两个不相等的负实数根,
有两个不相等的负实数根,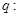 方程
方程 无实数根.
无实数根.
(Ⅰ)若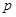 为真,求实数
为真,求实数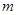 的取值范围;
的取值范围;
(Ⅱ)若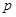 为假
为假 为真,求实数
为真,求实数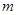 的取值范围.
的取值范围.
(本小题满分14分)已知函数 (其中
(其中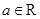 ,无理数
,无理数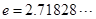 ).当
).当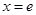 时,函数
时,函数 有极大值
有极大值 .
.
(1)求实数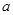 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)任取 ,
,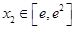 ,证明:
,证明: .
.
(本小题满分14分)平面内一动点 到定点
到定点 和到定直线
和到定直线 的距离相等,设
的距离相等,设 的轨迹是曲线
的轨迹是曲线 .
.
(1)求曲线 的方程;
的方程;
(2)在曲线 上找一点
上找一点 ,使得点
,使得点 到直线
到直线 的距离最短,求出
的距离最短,求出 点的坐标;
点的坐标;
(3)设直线
 ,问当实数
,问当实数 为何值时,直线
为何值时,直线 与曲线
与曲线 有交点?
有交点?
(本小题满分14分)北京市周边某工厂生产甲、乙两种产品.一天中,生产一吨甲产品、一吨乙产品所需要的煤、水以及产值如表所示:
| 用煤(吨) |
用水(吨) |
产值(万元) |
|
| 生产一吨甲种产品 |
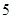 |
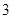 |
 |
| 生产一吨乙种产品 |
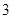 |
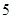 |
 |
在 会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多
会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多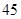 吨,用水最多
吨,用水最多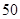 吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?