已知函数
．
（Ⅰ）求函数
的最小正周期；
（Ⅱ）将函数的图象向右平移
个单位长度，再向下平移
（
）个单位长度后得到函数
的图象，且函数的最大值为2．
（ⅰ）求函数的解析式；
（ⅱ）证明：存在无穷多个互不相同的正整数
，使得
．
已知点P在圆x2＋y2＝1上运动，过点P作x轴的垂线，垂足为D，点M在DP的延长线上，且有|DP|＝|MP|.(1)求M点的轨迹方程C；(2)已知直线l过点(0，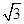
)，且斜率为1，求l与C相交所得的弦长．
如图所示，在四棱锥P—ABCD中，底面ABCD是边长为a的正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD，且PA＝PD＝
AD．
(1)求证：EF∥平面PAD；
(2)求证：平面PAB⊥平面PCD．
已知数列{an}是等差数列，且a3＝5，a2＋a7＝16.
(1)求数列{an}的通项公式；
(2)设bn＝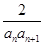
，求数列{bn}的前
项和Sn．
已知函数f(x)＝log4(2x＋3－x2)．
(1)求f(x)的定义域；
(2) 求f(x)的单调区间．
已知函数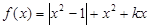
，且定义域为（0，2）.
(1）求关于x的方程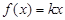
+3在（0，2）上的解；
（2）若
是定义域(0，2)上的单调函数，求实数
的取值范围；
（3）若关于x的方程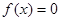
在（0，2）上有两个不同的解
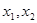，求k的取值范围。