某实验室一天的温度(单位: )随时间
)随时间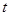 (单位:
(单位: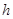 )的变化近似满足函数关系;
)的变化近似满足函数关系;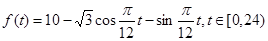 .
.
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11 ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
火车站对乘客退票收取一定的费用,具体办法是:按票价每10元(不足10元按10元计算)核收2元;2元以下的票不退.试写出票价为x元的车票退掉后,返还的金额y元的算法的程序框图.
如果学生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”.用程序框图表示这一算法过程.
某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算:
f=
其中 (单位:元)为托运费,ω为托运物品的重量(单位:千克),试写出一个计算费用
(单位:元)为托运费,ω为托运物品的重量(单位:千克),试写出一个计算费用 算法,并画出相应的程序框图.
算法,并画出相应的程序框图.
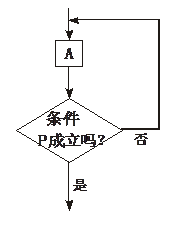
下面循环结构的程序框图中,哪一个是当型循环的程序框图?哪一个是直到型循环的程序框图?
(1)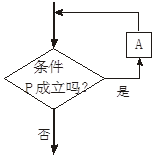
(2)
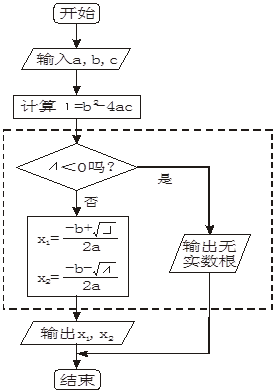
下面是描述求一元二次方程ax2+bx+c=0的根的过程的程序框图,请问虚线框内是什么结构?