某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：
f=
其中
（单位：元）为托运费，ω为托运物品的重量（单位：千克），试写出一个计算费用算法，并画出相应的程序框图.
（本小题满分14分）已知集合
是满足下列性质的函数
的全体：对于定义域B中的任何两个自变量
，都有
。（1）当B=R时，
是否属于？为什么？（2）当B=
时，
是否属于，若属于请给予证明；若
不属于说明理由，并说明是否存在一个
使属于
？
（文）（本小题满分12分）已知y=f(x)是偶函数，当x>0时，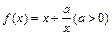
，
且当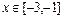
时，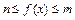
恒成立，若a≥9，求
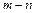的最小值．
（理）（本小题满分12分）已知y=f(x)是偶函数，当x>0时，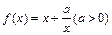
，
且当
时，
恒成立，求
的最小值．
（本小题满分12分）设函数
(a为实数).
（1）若a<0,用函数单调性定义证明:
在
上是增函数;
（2）若a=0,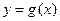
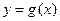的图象与的图象关于直线y=x对称,求函数的解析式.
（本小题满分12分）已知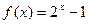
的反函数为
，
.
(1)若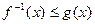
，求
的取值范围D；
(2)设函数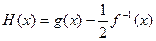
，当
时，求函数
的值域.