已知函数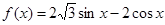
(Ⅰ)若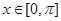 ,求
,求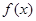 的最大值和最小值;
的最大值和最小值;
(Ⅱ)若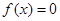 ,求
,求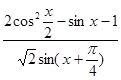 的值.
的值.
如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F为CD中点.
(Ⅰ)求证:EF⊥平面BCD;
(Ⅱ)求二面角C-DE-A的大小.
某学校有甲、乙、丙三名学生报名参加2012年高校自主招生考试,三位同学通过自主招生考试考上大学的概率分别是 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。
(Ⅰ)求恰有一位同学通过高校自主招生考试的概率;
(Ⅱ)若没有通过自主招生考试,还可以参加2012年6月的全国统一考试,且每位同学通过考试的概率均为 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。
在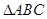 中,角
中,角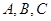 的对边分别为
的对边分别为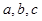 .
.
(Ⅰ)若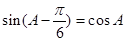 ,求角
,求角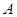 的大小;
的大小;
(Ⅱ)若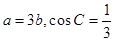 ,求
,求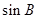 的值.
的值.
已知椭圆 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切.
(1)求椭圆 及动圆圆心轨迹
及动圆圆心轨迹 的方程;
的方程;
(2) 在曲线 上有两点
上有两点 、
、 ,椭圆
,椭圆 上有两点
上有两点 、
、 ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
已知函数 ,
, .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.