选修4-5:不等式选讲
设a,b,c均为正数,且a+b+c=1,证明:
(Ⅰ)ab+bc+ac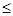
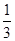 ;
;
(Ⅱ)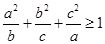 .
.
一个多面体的直观图和三视图如下: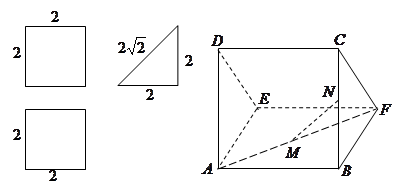
(其中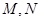 分别是
分别是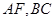 中点)
中点)
(1)求证: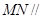 平面
平面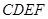 ;
;
(2)求多面体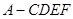 的体积.
的体积.
f(x)=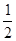 x2+
x2+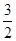 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令bn=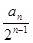 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD,底面ABCD是菱形,∠A=60°,E是AD的中点,F是PC的中点.
(Ⅰ)求证:BE⊥平面PAD;
(Ⅱ)求证:EF∥平面PAB;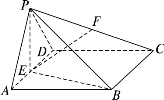
设函数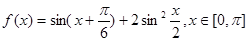 (Ⅰ)求
(Ⅰ)求 的值域;
的值域;
(Ⅱ)记 BC的内角A.B.C的对边长分别为
BC的内角A.B.C的对边长分别为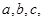
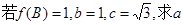 的值。
的值。
已知函数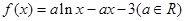
(1)当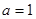 时,求函数
时,求函数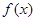 的单调区间;
的单调区间;
(2)若函数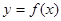 的图像在点
的图像在点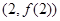 处的切线的倾斜角为
处的切线的倾斜角为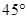 ,问:
,问: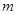 在什么范围取值时,函数
在什么范围取值时,函数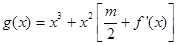 在区间
在区间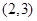 上总存在极值?
上总存在极值?
(3)当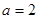 时,设函数
时,设函数 ,若对任意地
,若对任意地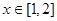 ,
,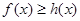 恒成立,求实数
恒成立,求实数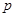 的取值范围
的取值范围