阅读材料：对于任何数，我们规定符号
的意义是
．
例如：
．
（1）按照这个规定，请你计算
的值．
（2）按照这个规定，请你计算当
时，
值．
某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：
| 类型价格 |
进价（元/盏） |
售价（元/盏） |
| A型 |
30 |
45 |
| B型 |
50 |
70 |
（1）若商场预计进货款为3500元，则这两种台灯各购进多少盏？
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
如图，某中学教学楼BM上有一宣传牌AB，为了测量AB的高度，先在地面上用测角仪自C处测得宣传牌底部B的仰角是37°，然后将测角仪向教学楼方向移动了4m到达点F处，此时自E处测得宣传牌的顶部A的仰角为45°．已知测角仪的高度是1m，教学楼高17米，且点D，F、M在同一直线上，求宣传牌AB的高度（结果精确到0．1m，参考数据：sin37°≈0．60，cos37°≈0．81，tan37°≈0．75）．
为了建设“魅力校园”，某学校准备推广由学生自行设计的礼仪校服．学生会设计了如图1的调查问卷，在全校学生中进行了一次调查，统计整理相关数据并绘制了如下两幅不完整的统计图（图2，图3）．请根据图中信息，解答下列问题：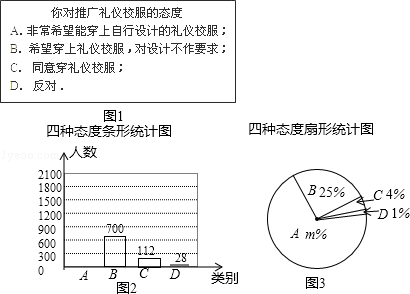
（1）计算扇形统计图3中m=；
（2）该校有名学生支持选项A，补全条形统计图2；
（3）若要从该校某班支持选项A的50名学生中随机选择一名同学试穿礼仪校服，则该班支持选项A的小美同学被选中的概率是多少？
（1）计算：（π﹣3．14）0+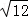
﹣（
）﹣1﹣2sin60°．
（2）先化简，再求值：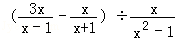
，其中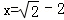
．
如图，四边形ABCD是矩形，AB＝6，BC＝8，点E在线段AD上，把△ABE沿直线BE翻折，点A落在点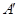
，
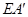的延长线交BC于点F，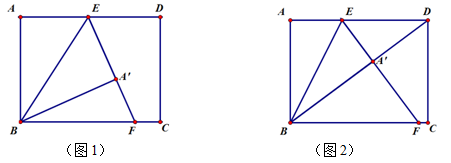
（1）如图（1）求证FE＝FB；
（2）当点E在边AD上移动时，点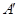的位置也随之变化，
①当点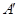恰好落在线段BD上时，如图（2），求AE的长；
②在运动变化过程中，设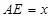
，
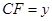，求
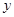与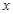
的函数关系式，试判断
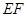能否平分矩形ABCD的面积，若能，求出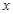的值，若不能，则说明理由；
（3）当点E在边AD上运动时，点D与点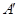之间的距离也随之变化，请直接写出点D与点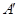之间距离的变化范围．