基本模型
如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE∽△BCF.
(1)模型拓展:
如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE∽△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4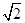 ,E,F分别是AC,AB上的一点,若∠CFE=45°.若设AE=y,BF=x,求出y与x的函数关系式及y的最大值;
,E,F分别是AC,AB上的一点,若∠CFE=45°.若设AE=y,BF=x,求出y与x的函数关系式及y的最大值;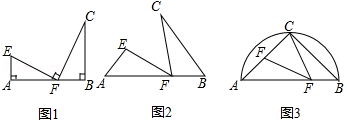
如图,某高速公路建设中需要确定隧道AB的长度.当飞机在离地面高度CE=1500m时,测量人员从C处测得A、B两点处的俯角分别为60°和45°.求隧道AB的长( ≈1.732,结果保留整数).
≈1.732,结果保留整数).
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在
AC的延长线上,且∠CBF= ∠CAB.
∠CAB.
(Ⅰ)求证:直线BF是⊙O的切线;
(Ⅱ)若AB=5,sin∠CBF= ,求BC和BF的长.
,求BC和BF的长.
在一副扑克牌中取牌面花色分别为黑桃、红心、方块各一张,洗匀后正面朝下放在桌面上.
(Ⅰ)从这三张牌中随机抽取一张牌,抽到牌面花色为红心的概率是多少?
(Ⅱ)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面花色后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面花色.当两张牌的花色相同时,小王赢;当两张牌面的花色不相同时,小李赢.请你利用树形图或列表法分析该游戏规则对双方是否公平?并说明理由.
如图,在平面直角坐标系中,一次函数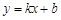 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E.已知点C的坐标是(6,-1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E.已知点C的坐标是(6,-1),DE=3.
(Ⅰ)求反比例函数与一次函数的解析式.
(Ⅱ)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
解方程组 