已知关于x的方程x2－6x＋m2－3m＝0的一根为2．
（1）求5m2－15m－100的值；
（2）求方程的另一根．
完成证明并写出推理根据：
已知，如图，∠1＝132o，∠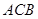
＝48o，∠2＝∠3，
⊥
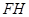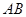于
，
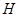求证：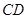
⊥．
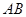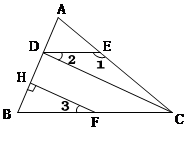
证明：∵∠1＝132o，∠ACB＝48o，
∴∠1＋∠ACB＝180°
∴DE∥BC
∴∠2＝∠DCB（____________________________）
又∵∠2＝∠3
∴∠3＝∠DCB
∴HF∥DC（____________________________）
∴∠CDB=∠FHB．（____________________________）
又∵FH⊥AB，
∴∠FHB=90°（____________________________）
∴∠CDB=________°．
∴CD⊥AB．（____________________________）
如图，点A在∠O的一边OA上．按要求画图并填空：
（1）过点A画直线AB ⊥OA，与∠O的另一边相交于点B；
（2）过点A画OB的垂线段AC，垂足为点C；
（3）过点C画直线CD∥OA ，交直线AB于点D；
（4）∠CDB=°；
（5）如果OA=8，AB=6，OB=10，则点A到直线OB的距离为．
某地为更好治理湖水水质，治污部门决定购买10台污水处理设备．现有
两种型号的设备，其中每台的价格，月处理污水量如下表：
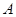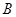 型 |
 型 |
|
| 价格（万元/台） |
 |
 |
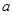| 处理污水量（吨/月） |
240 |
200 |
经调查：购买一台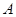型设备比购买一台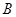型设备多2万元，购买2台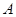型设备比购买3台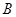型设备少6万元．
（1）求
的值．
（2）经预算：治污部门购买污水处理设备的资金不超过105万元，你认为该部门有哪几种购买方案．
（3）在（2）问的条件下，若每月要求处理的污水量不低于2040吨，为了节约资金，请你为治污部门设计一种最省钱的购买方案．
已知：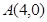
，
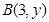，点
在
轴上，
．
（1）直接写出点的坐标；
（2）若
，求点
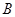的坐标．
解不等式组
，并写出该不等式组的整数解．