为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m(参考数据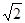 ≈1.41,
≈1.41,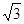 ≈1.73)
≈1.73)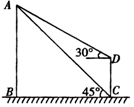
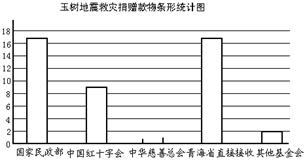
玉树地震后,全国人民慷慨解囊,积极支援玉树人民抗震救灾,他们有的直接捐款,有的捐物.国家民政部、中国红十字会、中华慈善总会及其他基金会分别接收了捐赠,青海省也直接接收了部分捐赠.截至5月14日12时,他们分别接收捐赠(含直接捐款数和捐赠物折款数)的比例见扇形统计图(图①),其中,中华慈善总会和中国红十字会共接收捐赠约合人民币15.6亿元.请你根据相关信息解决下列问题:
(1)其他基金会接收捐赠约占捐赠总数的百分比是;
(2)全国接收直接捐款数和捐物折款数共计约亿元;
(3)请你补全图②中的条形统计图;
(4)据统计,直接捐款数比捐赠物折款数的6倍还多3亿元,那么直接捐款数和捐赠物折款数各多少亿元?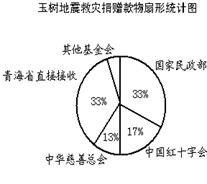
近期以来,大蒜和绿豆的市场价格离奇攀升,网民戏称为“蒜你狠”、“豆你玩”.以绿豆为例,5月上旬某市绿豆的市场价已达16元/千克.市政府决定采取价格临时干预措施,调进绿豆以平抑市场价格.经市场调研预测,该市每调进100吨绿豆,市场价格就下降1元/千克.为了即能平抑绿豆的市场价格,又要保护豆农的生产积极性,绿豆的市场价格控制在8元/千克到10元/千克之间(含8元/千克和10元/千克).问调进绿豆的吨数应在什么范围内为宜?
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连结EF,试判断四边形BCEF的形状,并说明理由.
学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长提出由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由.
已知
,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:
(1)作
的平分线
交
于点
;
(2)作线段
的垂直平分线交
于点
,交
于点
.由
、
可得:线段
与线段
的关系为