如图,一次函数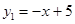 与反比例函数
与反比例函数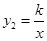 的图象交于
的图象交于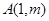 、
、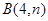 两点.
两点.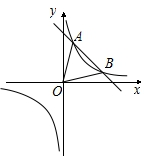
(1)求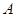 、
、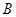 两点的坐标和反比例函数的解析式;
两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当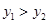 时
时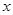 的取值范围;
的取值范围;
(3)求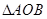 的面积.
的面积.
如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

已知关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)当 时,方程的两根分别是矩形的长和宽,求该矩形外接圆的直径.
如图,在 中, , , , 、 分别是斜边 、直角边 上的点,把 沿着直线 折叠.

(1)如图1,当折叠后点 和点 重合时,用直尺和圆规作出直线 ;(不写作法和证明,保留作图痕迹)
(2)如图2,当折叠后点 落在 边上点 处,且四边形 是菱形时,求折痕 的长.
某校举办“打造平安校园”活动,随机抽取了部分学生进行校园安全知识测试.将这些学生的测试结果分为四个等级: 级:优秀; 级:良好; 级:及格; 级:不及格,并将测试结果绘制成如下统计图.请你根据图中信息,解答下列问题:
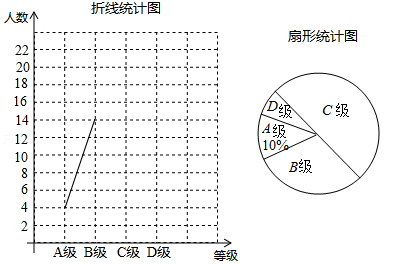
(1)本次参加校园安全知识测试的学生有多少人?
(2)计算 级所在扇形圆心角的度数,并补全折线统计图;
(3)若该校有学生1000名,请根据测试结果,估计该校达到及格和及格以上的学生共有多少人?
如图,在平面直角坐标系中,菱形 的边 在 轴上,点 坐标 ,点 在 轴正半轴上,且 ,点 从原点 出发,以每秒一个单位长度的速度沿 轴正方向移动,移动时间为 秒,过点 作平行于 轴的直线 ,直线 扫过四边形 的面积为 .
(1)求点 坐标.
(2)求 关于 的函数关系式.
(3)在直线 移动过程中, 上是否存在一点 ,使以 、 、 为顶点的三角形是等腰直角三角形?若存在,直接写出 点的坐标;若不存在,请说明理由.
