若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-
，x1•x2=
．把它称为一元二次方程根与系数关系定理．如果设二次函数y=ax2+bx+c（a≠0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．利用根与系数关系定理可以得到A、B两个交点间的距离为：AB=|x1-x2|=
；
参考以上定理和结论，解答下列问题：
设二次函数y=ax2+bx+c（a＞0）的图象与x轴的两个交点A（x1，0），B（x2，0），抛物线的顶点为C，显然△ABC为等腰三角形．
（1）当△ABC为直角三角形时，求b2-4ac的值；
（2）当△ABC为等边三角形时，求b2-4ac的值．
如图，在平面直角坐标系xOy中，直线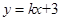
的图象与反比例函数
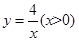的图象交于点A(1，m)，与x轴交于点
，过点A作
轴于点
．
（1）求一次函数的解析式；
（2）若P为x轴上一点，且△ABP的面积为10，直接写出点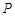
的坐标．
已知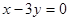
,求代数式
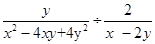的值．
已知：如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．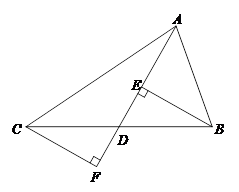
求证：BE=CF．
解不等式组：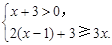
，抛物线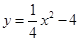
交x轴于点Q、M，交y轴于点P，点P关于x轴的对称点为N。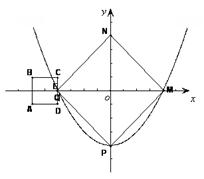
(1)求点M、N的坐标，并判断四边形NMPQ的形状；
(2)如图，坐标系中有一正方形ABCD，其中AB=2cm且CD⊥x轴，CD的中点E与Q点重合，正方形ABCD以1cm/s的速度沿射线QM运动，当正方形ABCD完全进入四边形QPMN时立即停止运动．
①当正方形ABCD与四边形NMPQ的交点个数为2时，求两四边形重叠部分的面积y与运动时间t之间的函数关系式，并写出自变量t的取值范围；
②求运动几秒时，重叠部分的面积为正方形ABCD面积
的一半．