数列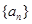 为公差不为
为公差不为 的等差数列,
的等差数列,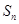 为前
为前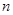 项和,
项和,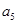 和
和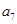 的等差中项为
的等差中项为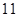 ,且
,且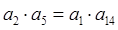 .令
.令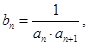 数列
数列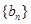 的前
的前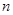 项和为
项和为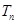 .
.
(Ⅰ)求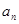 及
及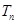 ;
;
(Ⅱ)是否存在正整数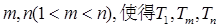 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的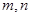 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知命题 :“直线
:“直线 与圆
与圆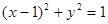 有公共点”,命题
有公共点”,命题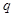 :函数
:函数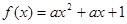 没有零点, 若命题
没有零点, 若命题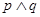 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数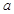 的取值范围.
的取值范围.
已知方程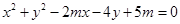 的曲线是圆C
的曲线是圆C
(1)求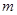 的取值范围;
的取值范围;
(2)当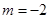 时,求圆C截直线
时,求圆C截直线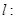
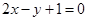 所得弦长;
所得弦长;
已知数列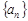 满足
满足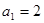 ,向量
,向量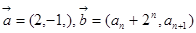 ,且
,且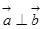 .
.
(Ⅰ)求证数列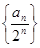 为等差数列,并求
为等差数列,并求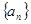 通项公式;
通项公式;
(Ⅱ)设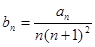 ,若对任意
,若对任意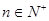 都有
都有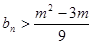 成立,求实数
成立,求实数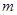 的取值范围.
的取值范围.
数列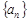 中,
中,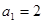 ,
,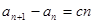 (c是常数,n=1,2,3,),且
(c是常数,n=1,2,3,),且 成公比不为1的等比数列.
成公比不为1的等比数列.
(1)求c的值;
(2)求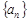 的通项公式.
的通项公式.
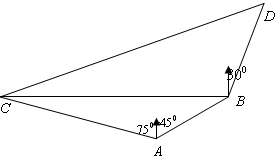
在海岸A处 ,发现北偏东450方向,距A处 海里B处有一艘走私船,在A处北偏西750方向,距A处2海里的C处的缉私船奉命以
海里B处有一艘走私船,在A处北偏西750方向,距A处2海里的C处的缉私船奉命以 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东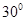 方向航行,问缉私船沿什么方向能最快追上走私船,并求出所需时间.
方向航行,问缉私船沿什么方向能最快追上走私船,并求出所需时间.