(Ⅰ)设 ,
,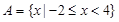 ,
,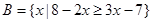 ,求
,求 .
.
(Ⅱ)已知集合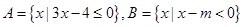 ,且
,且 ,求
,求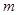 的取值范围.
的取值范围.
如图,在直三棱柱ABC—A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA。
(I)当k=1时,求证PA⊥B1C;
(II)当k为何值时,直线PA与平面BB1C1C所成的角的正弦值为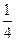 ,并求此时二面角A—PC—B的余弦值。
,并求此时二面角A—PC—B的余弦值。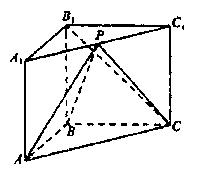
(本小题满分12分)
某汽车驾驶学校在学员结业前对其驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核, 若小张参加每次考核合格的概率依次组成一个公差为
若小张参加每次考核合格的概率依次组成一个公差为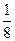 的等差数列,他参加第一次考核合格的概率超过
的等差数列,他参加第一次考核合格的概率超过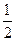 ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为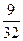
(I)求小张第一次参加考核就合格的概率P1;
(Ⅱ)求小张参加考核的次数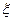 和分布列和数学期望值
和分布列和数学期望值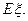
(本小题满分10分)
在△ABC中,内角A、B、C对边长分别是a,b,c,已知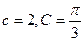
(I)若△ABC的面积等于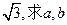 ;
;
(II)若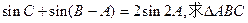 的面积。
的面积。
(本小题满分14分)
已知函数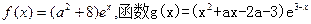
(1)若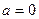 ,求
,求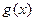 的单调递减区间;
的单调递减区间;
(2)若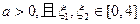 ,求
,求 的最小值;
的最小值;
(3)若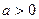 ,且存在
,且存在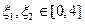 使得
使得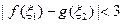 ,求实数
,求实数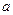 的取值范围。
的取值范围。
(本小题满分14分)
如图,F1、F2分别是椭圆 的左右焦点,M为椭圆上一点,MF2垂直于
的左右焦点,M为椭圆上一点,MF2垂直于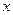 轴,椭圆下顶点和右顶点分别为A,B,且
轴,椭圆下顶点和右顶点分别为A,B,且
(1)求椭圆的离心率;
(2)过F2作OM垂直的直线交椭圆于点P,Q,若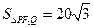 ,求椭圆方程。
,求椭圆方程。