(本小题满分12分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组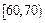 ,…,第五组
,…,第五组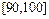 .下图是按上述分组方法得到的频率分布直方图。
.下图是按上述分组方法得到的频率分布直方图。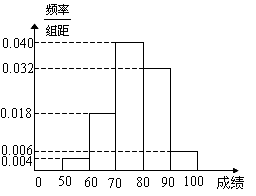
(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩
合格的人数;
(Ⅱ)从测试成绩在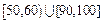 内的所有学生中随机抽取两名同学,设其测试成绩分别为
内的所有学生中随机抽取两名同学,设其测试成绩分别为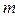 ,
, ,求事件“
,求事件“ ”概率.
”概率.
(本小题满分12分)在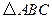 中,
中,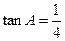 ,
,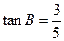 .
.
(Ⅰ)求角 的大小; (Ⅱ)若
的大小; (Ⅱ)若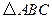 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
(本小题满分14分)已知函数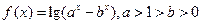
(1)求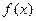 的定义域;
的定义域;
(2)在函数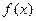 的图象上是否存在不同的两点,使过这两点的直线平行于
的图象上是否存在不同的两点,使过这两点的直线平行于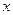 轴;
轴;
(3)当 满足什么条件时,
满足什么条件时,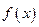 在
在 上恒取正值.
上恒取正值.
(本小题满分为14分)定义在(-1,1)上的函数 满足:
满足:
①对任意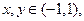 都有
都有 ;
;
② 在
在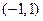 上是单调递增函数,
上是单调递增函数, .
.
(1)求 的值;
的值;
(2)证明 为奇函数;
为奇函数;
(3)解不等式 .
.
(本小题满分13分).某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是: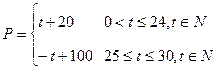
该商品的日销售量Q(件)与时间(天)的函数关系是:Q=-t+40 (0<t≤30,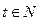 ),
),
求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?