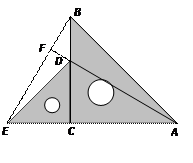
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
已知:点到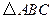 的两边
的两边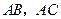 所在直线的距离相等,且
所在直线的距离相等,且 .
.
(1)如图,若点在边 上,求证:
上,求证: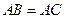 ;
;
(2)如图,若点在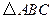 的内部,求证:
的内部,求证: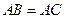 ;
;
(3)若点在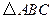 的外部,
的外部,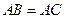 成立吗?请画图表示.
成立吗?请画图表示.
(10分)康乐公司在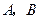 两地分别有同型号的机器
两地分别有同型号的机器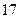 台和
台和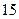 台,现要运往甲地
台,现要运往甲地 台,乙地
台,乙地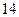 台,从
台,从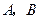 两地运往甲、乙两地的费用如下表:
两地运往甲、乙两地的费用如下表:
| 甲地(元/台) |
乙地(元/台) |
|
| 地 |
 |
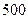 |
| 地 |
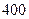 |
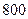 |
(1)如果从地运往甲地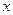 台,求完成以上调运所需总费用
台,求完成以上调运所需总费用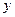 (元)与
(元)与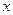 (台)之间的函数关系式;
(台)之间的函数关系式;
(2)请你为康乐公司设计一种最佳调运方案,使总费用最少,并说明理由。
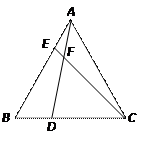
(10分)如图,在等边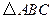 中,点
中,点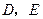 分别在边
分别在边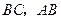 上,且
上,且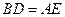 ,
,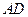 与
与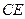 交于点
交于点 .
.
(1)求证: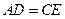 ;
;
(2)求 的度数.
的度数.
(9分)在市区内,我市乘坐出租车的价格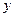 (元)与路程
(元)与路程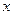 (km)的函数关系图象如图所示.
(km)的函数关系图象如图所示.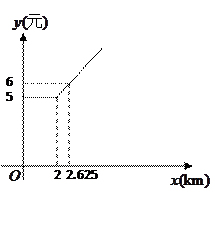
(1)请你根据图象写出两条信息;
(2)小明从学校出发乘坐出租车回家用了13元,求学校离小明家的路程.
(9分)把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.
求证:AF⊥BE.