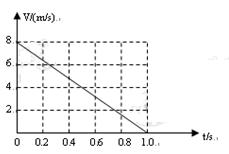
如图所示，K与虚线MN之间是加速电场，虚线MN与PQ之间是匀强电场，虚线PQ与荧光屏之间是匀强磁场，且MN、PQ与荧光屏三者互相平行，电场和磁场的方向如图所示，图中A点与O点的连线垂直于荧光屏。一带正电的粒子从A点离开加速电场，速度方向垂直于偏转电场方向射入偏转电场，在离开偏转电场后进入匀强磁场，最后恰好垂直地打在荧光屏上。已知电场和磁场区域在竖直方向足够长，加速电场电压与偏转电场的场强关系为U=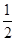
Ed，式中的d是偏转电场的宽度，磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=
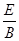。若题中只有偏转电场的宽度d为已知量。
（1）画出带电粒子轨迹示意图。
（2）磁场的宽度L为多少？
（3）带电粒子在电场和磁场中垂直于v0方向的偏转距离分别是多少？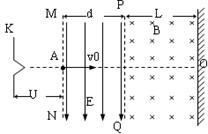
如图甲所示，一质量为m、电荷量为q的正离子，在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中，此磁场方向垂直纸面向里．结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场，此电场方向与AC平行且向上，最后离子打在G处，而G处到A点的距离为2d（直线DAG与电场方向垂直）．不计离子重力，离子运动轨迹在纸面内．求：
（1）正离子从D处运动到G处所需时间．
（2）正离子到达G处时的动能．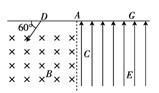
一位蹦床运动员仅在竖直方向上运动，蹦床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来，如图所示。设运动过程中不计空气阻力，g取10m/s2。结合图象，试求：
（1）运动员的质量m；
（2）运动过程中，运动员的最大加速度；
（3）运动员离开蹦床上升的最大高度。
在如图17所示的坐标系中，x 轴沿水平方向，y 轴沿竖直方向.第二象限内存在沿 y 轴负方向的匀强电场，在第三象限内存在垂直 xy 平面（纸面）向里的匀强磁场.一质量为m 、电量为q的带正电粒子（不计重力），从y 轴上的A点以v0的初速度沿x 轴负方向进入第二象限，之后到达x轴上x＝ – 2h处的B点，带电粒子在 B点的速度方向与x轴负方向成 450 角，进入第三象限后粒子做匀速圆周运动，恰好经过y 轴上y ＝ –2h处的C点。求：
⑴ 粒子到达B点时速度大小；
⑵ 第二象限中匀强电场的电场强度的大小；
⑶ 第三象限中磁感应强度的大小和粒子在磁场中的运动时间.
如图16所示，足够长的光滑水平面上，轻弹簧两端分别拴住质量均为m 的小物块A 和B ，B物块靠着竖直墙壁。今用水平外力缓慢推A ，使A 、B间弹簧压缩，当压缩到弹簧的弹性势能为E时撤去此水平外力，让A和B在水平面上运动。
求：
⑴ 当B刚离开墙壁时，A物块的速度大小；
⑵ 当弹簧达到最大长度时A、B的速度大小；
⑶ 当B离开墙壁以后的运动过程中，弹簧弹性势能的最大值．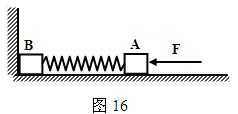
一质量m ＝ 2.0 kg的小物块以一定的初速度冲上一个足够长的倾角为37º的固定斜面，某同学利用传感器测出了小物
块冲上斜面过程中多个时刻的瞬时速度，并用计算机做出了小物块上滑过程的速度～时间
图线，如图15所示。（取sin 37º＝0.6 ，
Cos 37º＝0.8，g ＝10 m/s2）求：
⑴ 小物块冲上斜面过程中加速度的大小；
⑵ 小物块与斜面间的动摩擦因数；
⑶ 小物块向上运动的最大距离。