设数列
共有
项，记该数列前
项
中的最大项为
，该数列后
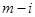项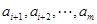
中的最小项为
，
．
（1）若数列的通项公式为
，求数列
的通项公式；
（2）若数列满足
，
，求数列的通项公式；
（3）试构造一个数列，满足
，其中
是公差不为零的等差数列，
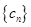是等比数列，使得对于任意给定的正整数
，数列都是单调递增的，并说明理由．
近年来,我国许多地方出现雾霾天气，影响了人们的出行、工作与健康．其形成与
有关. 是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物. 日均值越小，空气质量越好.为加强生态文明建设，我国国家环保部于2012年2月29日，发布了《环境空气质量标准》见下表：
| 日均值k(微克) |
空气质量等级 |
 |
一级 |
 |
二级 |
 |
超标 |
某环保部门为了了解甲、乙两市的空气质量状况，在某月中分别随机抽取了甲、乙两市6天的日均值作为样本，样本数据茎叶图如右图所示（十位为茎，个位为叶）．
（1）求甲、乙两市日均值的样本平均数，据此判断该月中哪个市的空气质量较好；
（2）若从甲市这6天的样本数据中随机抽取两天的数据，求恰有一天空气质量等级为一级的概率．
已知数列
为等差数列，且
．
（1）求数列
的通项公式；
（2）求证：
.
设函数
,
（1）求
的最小值
；
（2）当
时,求
的最小值.
在平面直角坐标系
中，以
为极点，
轴非负半轴为极轴建立坐标系，已知曲线
的极坐标方程为
，直线
的参数方程为:
（
为参数），两曲线相交于
两点.
（1）写出曲线的直角坐标方程和直线的普通方程；
（2）若
求
的值.
已知矩阵
，若矩阵
属于特征值6的一个特征向量为
，属于特征值1的一个特征向量
.
（1）求矩阵的逆矩阵；
（2）计算