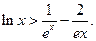已知函数 (
( ),其中
),其中 是自然对数的底数.
是自然对数的底数.
(1)当 时,求
时,求 的极值;
的极值;
(2)若 在
在 上是单调增函数,求
上是单调增函数,求 的取值范围;
的取值范围;
(3)当 时,求整数
时,求整数 的所有值,使方程
的所有值,使方程 在
在 上有解.
上有解.
设 ,其中
,其中 .
.
(1)当 时,求
时,求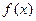 的极值点;
的极值点;
(2)若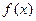 为R上的单调函数,求
为R上的单调函数,求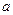 的取值范围.
的取值范围.
如图,四棱锥P—ABCD中,底面ABCD为平行四边形,
∠DAB=60°,AB=2AD=2,PD⊥底面ABCD.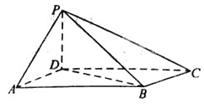
(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-P B-C的余弦值.
B-C的余弦值.
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13
后成为等比数列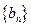 中的
中的 、
、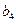 、
、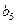 .
.
(1)求数列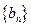 的通项公式;
的通项公式;
(2)数列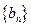 的前n项和为
的前n项和为 ,求证:数列
,求证:数列 是等比数列.
是等比数列.
已知函数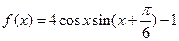 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分14分)已知函数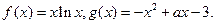
(I)求函数 在
在
 上的最小值;
上的最小值;
(II)对一切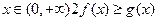 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(III)求证:对一切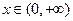 ,都有
,都有