“双十一”淘宝网销售一款工艺品，每件的成本是50元．销售期间发现：销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件．但要求销售单价不得低于成本．设当销售单价为x元时，每天的销售利润为y元．
（1）求出y与x之间的函数表达式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果每天的销售利润不低于4000元，那么每天的总成本至少需要 元．
（每天的总成本=每件的成本×每天的销售量）
．解方程： 
分解因式（1）
(5分)
（2）
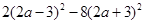(5分)
某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行，并以各自的速度匀速行驶， 1.5小时时甲车先到达配货站C地，此时两车相距30千米，甲车在C地用1小时配货，然后按原速度开往B地；2小时时乙车也到达C地，乙车未停留直接开往A地．乙车的速度是千米/小时，B、C两地的距离是千米，A、C两地的距离是千米；
（2）求甲车的速度及甲车到达B地所用的时间；
（3）乙车出发多长时间，两车相距150千米？
（本题8分）小明家使用的是分时电表，按平时段（6：00－22：00）和谷时段（22：00－次日6：00）分别计费，平时段每度电价为0.61元，谷时段每度电价为0.30元，小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示（如图7），同时将前4个月的用电量和相应电费制成表格（如表1）
根据上述信息，解答下列问题：
（1）计算5月份的用电量和相应电费，将所得结果填入表1中；
（2）小明家这5个月的月平均用电量为 度；
（3）小明家这5个月的月平均用电量呈 趋势（选择“上升”或“下降”）；这5个月每月电费呈 趋势（选择“上升”或“下降”）；
（4）
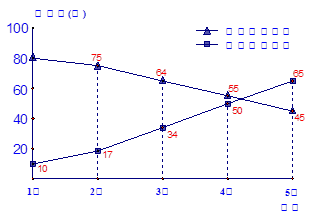小明预计7月份家中用电量很大，估计7月份用电量可达500度，相应电费将达243元，请你根据小明的估计，计算出7月份小明家平时段用电量和谷时段用电量.
| 月用电量（度） |
电费（元） |
|
| 1月 |
90 |
51.80 |
| 2月 |
92 |
50.85 |
| 3月 |
98 |
49.24 |
| 4月 |
105 |
48.55 |
| 5月 |
右图是由几个小正方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小正方块的个数，请画出这个几何体的主视图和左视图