选修4-4:极坐标系与参数方程
极坐标系的极点为直角坐标系 的原点,极轴为x轴的正半轴,两坐标系的长度单位相同。已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两坐标系的长度单位相同。已知曲线C的极坐标方程为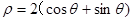 ,斜率为
,斜率为 的直线
的直线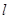 交y轴于点E(0,1).
交y轴于点E(0,1).
(1)求曲线C的直角坐标方程,直线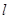 的参数方程;
的参数方程;
(2)若直线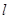 与曲线C交于A,B两点,求
与曲线C交于A,B两点,求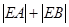 的值。
的值。
为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》,某驾校将小型汽车驾照考试科目二的培训测试调整为:从10个备选测试项目中随机抽取4个,只有选中的4个项目均测试合格,科目二的培训才算通过.已知甲对10个测试项目测试合格的概率均为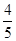 ;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
(Ⅰ)求甲恰有2个测试项目合格的概率;
(Ⅱ)记乙的测试项目合格数为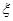 ,求
,求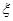 的分布列及数学期望
的分布列及数学期望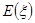 .
.
如图,三棱柱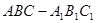 侧棱与底面垂直,且所有棱长都为4,D为CC1中点.
侧棱与底面垂直,且所有棱长都为4,D为CC1中点.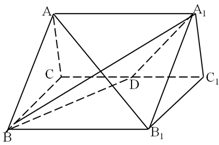
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
若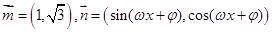 (
( ,
,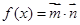 ,已知点
,已知点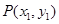 ,
,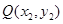 是函数
是函数 图象上的任意两点,若
图象上的任意两点,若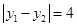 时,
时,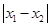 的最小值为
的最小值为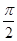 ,且函数
,且函数 为奇函数.
为奇函数.
(Ⅰ)求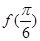 的值;
的值;
(Ⅱ)将函数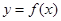 的图象向右平移
的图象向右平移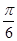 个单位后,得到函数
个单位后,得到函数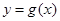 的图象,求函数
的图象,求函数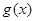 的单调递增区间.
的单调递增区间.
已知函数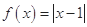 .
.
(1)解不等式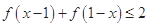 ;
;
(2)若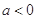 ,求证:
,求证: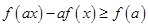
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系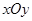 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为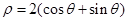 ,斜率为
,斜率为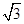 的直线
的直线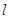 交y轴于点
交y轴于点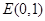 .
.
(1)求C的直角坐标方程,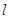 的参数方程;
的参数方程;
(2)直线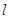 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求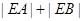 .
.