已知椭圆 :
: (
( )的离心率
)的离心率 ,且过点
,且过点 .
.
(1)求椭圆 的方程;
的方程;
(2)如果直线 (
( R)与椭圆相交于
R)与椭圆相交于 、
、 ,若
,若 ,
,  ,求证:直线
,求证:直线 与直线
与直线 的交点
的交点 必在一条确定的双曲线上;
必在一条确定的双曲线上;
(3)若直线 经过椭圆
经过椭圆 的左焦点交椭圆
的左焦点交椭圆 于
于 、
、 两点,
两点,  为坐标原点,且
为坐标原点,且 ,求直线
,求直线 的方程.
的方程.
设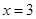 是函数
是函数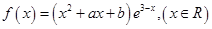 的一个极值点。
的一个极值点。
(1)求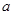 与
与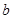 的关系式(用
的关系式(用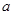 表示
表示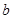 ),并求
),并求 的单调区间;
的单调区间;
(2)设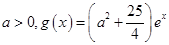 ,若存在
,若存在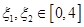 ,使得
,使得 成立,求实数
成立,求实数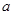 的取值范围。
的取值范围。
过点 的直线
的直线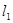 交直线
交直线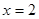 于
于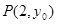 ,过点
,过点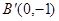 的直线
的直线 交
交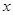 轴于
轴于 点,
点, ,
, .
.
(1)求动点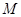 的轨迹
的轨迹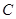 的方程;
的方程;
(2)设直线l与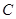 相交于不同的两点
相交于不同的两点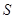 、
、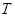 ,已知点
,已知点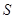 的坐标为(-2,0),点Q(0,
的坐标为(-2,0),点Q(0, )在线段
)在线段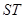 的垂直平分线上且
的垂直平分线上且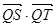 ≤4,求实数
≤4,求实数 的取值范围.
的取值范围.
已知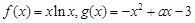 .
.
(1)已知函数h(x)=g(x)+ax3的一个极值点为1,求a的取值;
(2) 求函数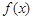 在
在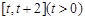 上的最小值;
上的最小值;
(3)对一切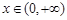 ,
,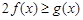 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知函数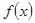 是定义在
是定义在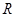 上的偶函数,且当
上的偶函数,且当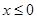 时,
时,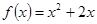 .现已画出函数
.现已画出函数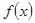 在
在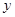 轴左侧的图像,如图所示,并根据图像
轴左侧的图像,如图所示,并根据图像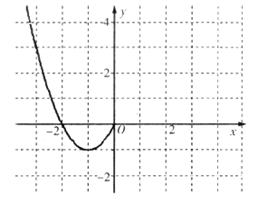
(1)写出函数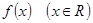 的增区间;
的增区间;
(2)写出函数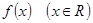 的解析式;
的解析式;
(3)若函数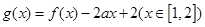 ,求函数
,求函数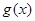 的最小值。
的最小值。
已知函数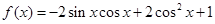
(1)设方程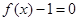 在(0,
在(0,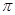 )内有两个零点
)内有两个零点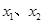 ,求
,求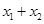 的值;
的值;
(2)若把函数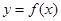 的图像向左移动
的图像向左移动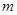
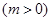 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于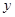 轴对称,求
轴对称,求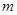 的最小值。
的最小值。